Using DataRobot and DataRobot API
Introduction
In this blog post, we demonstrate how to use Python and the DataRobot API (visit our full API Documentation) to quantify and visualize the expected distribution for predictions that fall into different patient readmission probability ranges at our subject hospital.
A single readmission prediction is a model’s best guess, but doesn’t include the distribution of possible predictions that occur from sampling biases typically found in the training data. Ideally, training data are an unbiased and representative sample of the entire population, but since the datasets are only a sample, they will contain biases. Modeling will ultimately fit to those sampling biases.
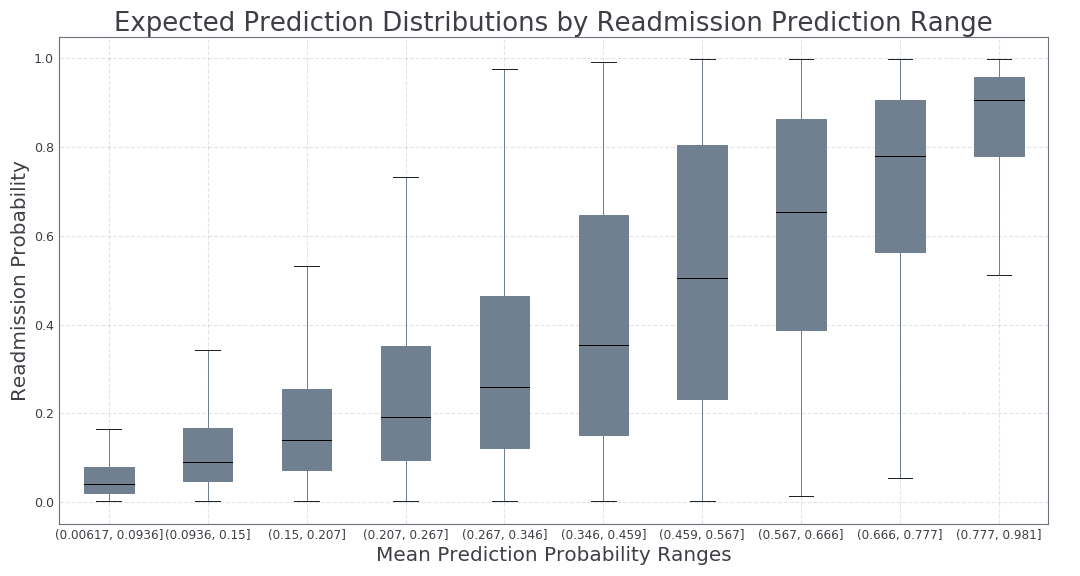 These prediction distributions can be used to assess model confidence, make directed improvements to the model, and ultimately make decisions on new data with a sense of prediction confidence.
These prediction distributions can be used to assess model confidence, make directed improvements to the model, and ultimately make decisions on new data with a sense of prediction confidence.
Bootstrapping, a method that relies on random sampling with replacement, allows us to assign a measure of the prediction reproducibility by creating a distribution of training data for modeling. Models are built by fitting to each training dataset, and will yield different predictions. The basic idea of bootstrapping for assessing prediction distributions is that the distributions about the population can be modeled by resampling the training data and performing inference about a sample from the resampled data. The training data become the population and the resampled data become the samples. As the population is unknown, the true error in a sample statistic against its population value is unknown. In bootstrap-resamples, the ‘population’ is in fact the sample, and this is known; hence the quality of inference of the ‘true’ sample from resampled data is measurable.
Knowing the prediction distribution adds another layer of information and confidence in the model that can be used to make better decisions. For example, if the model predicts a readmission probability of 0.4, hospital administrators may not take any actions. But, if the confidence of predictions in the range of 0.4 is poor, the hospital may take a different action to avoid a costly false negative. On the other hand, modelers can use this information to interpret the robustness or certainty of the given model over the entire range of predictions. They can make model improvements, acquire more data, or determine that the model is stable and robust for certain ranges of predictions, leading administrators to conclude that no further development is required.
The following method shows us how to use DataRobot to empirically estimate the prediction distributions for each range of predicted probabilities.
Background and Objectives
Use Case:
-
Predict the probability of patient readmission within the next 30 days.
-
Hospitals are interested in predicting patient readmission probability due to fines levied for patient readmission within 30 days of discharge.
Method:
-
Train a model based on the historical readmission statistics captured in the 10K Diabetes training data.
-
The training data contains 10K patient examples that contain over 50 features.
-
The training data also indicates whether or not the patient was readmitted within 30 days of dismissal.
Main Objective:
Methodology
-
Load input data and initialize the DataRobot API client instance.
-
Create 100 bootstrapped datasets with a replacement from the original input data.
-
Using DataRobot’s automated machine learning API, build sets of models for each bootstrapped dataset.
-
Select the most accurate model fit on each bootstrapped dataset.
-
Using the best model, make predictions on the original dataset.
-
Sort and bin the predictions based on each record’s mean predicted probability.
-
Visualize the prediction intervals using boxplots.
Code
import datarobot as dr
import pandas as pd
pd.options.display.max_columns = 1000
import numpy as np
import time
import matplotlib.pyplot as plt
from jupyterthemes import jtplot
# currently installed theme will be used to set plot style if no arguments provided
jtplot.style()
get_ipython().magic(‘matplotlib inline’)
Load and Initialize DataRobot API Client Instance
# load input data
df = pd.read_csv(‘../demo_data/10kDiabetes.csv’)
# initialize datarobot client instance
dr.Client(config_path=‘/Users/benjamin.miller/.config/datarobot/my_drconfig.yaml’)
Bootstrapping
# create 100 samples with replacement from the original 10K diabetes dataset
samples = []
for i in range(100):
samples.append(df.sample(10000, replace=True))
Modeling
# loop through each sample dataframe
for i, s in enumerate(samples):
# initialize project
project = dr.Project.start(
project_name=‘API_Test_{}’.format(i+20),
sourcedata=s,
target=‘readmitted’,
worker_count=2
)
…Wait for modeling to complete for each bootstrapped sample
# get all projects
projects = []
for project in dr.Project.list():
if “API_Test” in project.project_name:
projects.append(project)
# *For each project…*
# Make predictions on the original dataset using the most accurate model
# initialize list of all predictions for consolidating results
bootstrap_predictions = []
# loop through each relevant project to get predictions on original input dataset
for project in projects:
# get best performing model
model = dr.Model.get(project=project.id, model_id=project.get_models()[0].id)
# upload dataset
new_data = project.upload_dataset(df)
# start a predict job
predict_job = model.request_predictions(new_data.id)
# get job status every 5 seconds and move on once ‘inprogress’
for i in range(100):
time.sleep(5)
try:
job_status = dr.PredictJob.get(
project_id=project.id,
predict_job_id=predict_job.id
).status
except: # normally the job_status would produce an error when it is completed
break
# now the predictions are finished
predictions = dr.PredictJob.get_predictions(
project_id=project.id,
predict_job_id=predict_job.id
)
# extract row ids and positive probabilities for all records and set to dictionary
pred_dict = {k: v for k, v in zip(predictions.row_id, predictions.positive_probability)}
# append prediction dictionary to bootstrap predictions
bootstrap_predictions.append(pred_dict)
Visualize the results
# combine all predictions into single dataframe with keys as ids
# each record is a row, each column is a set of predictions pertaining to
# a model created from a bootstrapped dataset
df_predictions = pd.DataFrame(bootstrap_predictions).T
# add mean predictions for each observation in df_predictions
df_predictions[‘mean’] = df_predictions.mean(axis=1)
# place each record into equal sized probability groups using the mean
df_predictions[‘probability_group’] = pd.qcut(df_predictions[‘mean’], 10)
# aggregate all predictions for each probability group
d = {} # dictionary to contain {Interval(probability_group): array([predictions])}
for pg in set(df_predictions.probability_group):
# combine all predictions for a given group
frame = df_predictions[df_predictions.probability_group == pg].iloc[:, 0:100]
d[str(pg)] = frame.as_matrix().flatten()
# create dataframe from all probability group predictions
df_pg = pd.DataFrame(d)
# create boxplots in order of increasing probability ranges
props = dict(boxes=‘slategray’, medians=‘black’, whiskers=‘slategray’)
viz = df_pg.plot.box(color=props, figsize=(15,7), patch_artist=True, rot=45)
grid = viz.grid(False, axis=‘x’)
ylab = viz.set_ylabel(‘Readmission Probability’)
xlab = viz.set_xlabel(‘Mean Prediction Probability Ranges’)
title = viz.set_title(
label=‘Expected Prediction Distributions by Readmission Prediction Range’,
fontsize=18
)
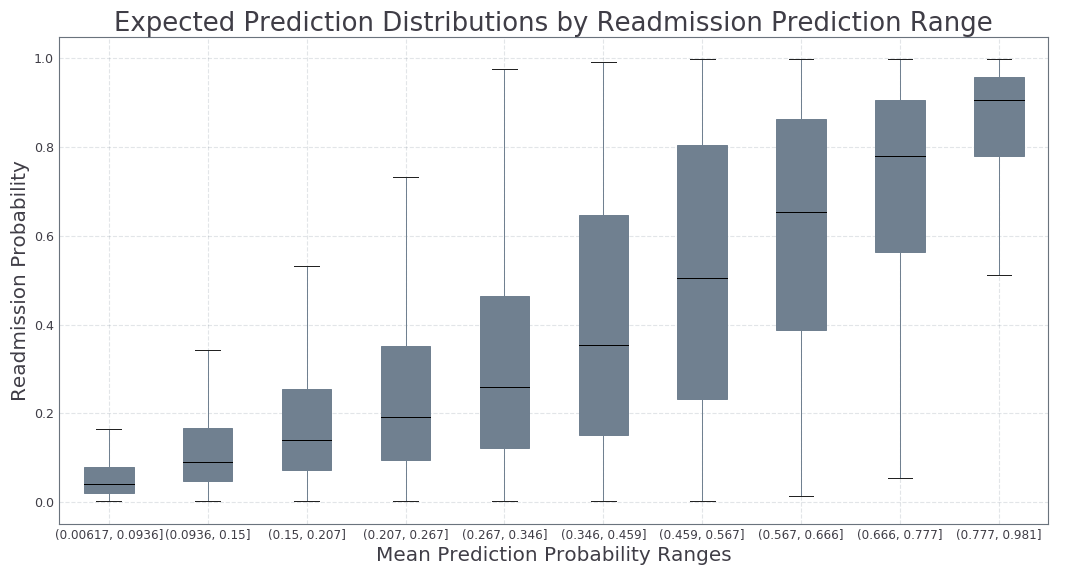
Results
At the upper and lower ends of the probability ranges, the prediction distributions are tighter. In the middle of the probability range, the distributions widen. The variance in the prediction distributions are widest for the hardest to classify records. This matches the intuition that it is much harder to predict what will happen on a borderline case. Based on this information, we expect to see more variability around the borderline cases, which would make it harder to trust a prediction in between 0.2 and 0.8. On the other hand, there is high confidence that a person with a high probability of readmission will in fact be readmitted. This information could be used to target the riskiest population with high confidence.
A note about this example…
The input dataset, while being based on real historical data, is only a small fraction of the full dataset. The prediction intervals would most likely decrease if the input dataset were larger. Also, I used full Autopilot to perform the modeling on each bootstrapped dataset, though a better approach would be to use a single model for each project. This would ensure a more “apples to apples” comparison. Choosing the best model is still appropriate, but could inflate the prediction intervals. Lastly, the predictions should be made on data not used in training any of the models. A holdout should have been separated at the start of the example. These holdout data should have been used for generating the predictions and assessing the expected prediction intervals.
Conclusion
Instead of a single probability, we can use this method to assess how confident we can be about the predictions made on new data. We can use this information to make decisions about how to handle each new case based on how much we can trust a single point prediction. Low risk individuals (P < 0.2) will most likely not be readmitted, while high risk individuals (P > 0.8) will likely need to be readmitted within the next 30 days. These results add another layer of information that administrators can use to make better decisions.

About the Author:
Ben Miller is a Customer Facing Data Scientist at DataRobot with a strong background in data science, advanced technology, and engineering. Ben is a machine learning professional with demonstrable skills in the area of multivariable regression, classification, clustering, predictive analytics, active learning, natural language processing, and algorithm R&D. He has scientific training and application in disparate industries including; biotechnology, life sciences, pharmaceutical, environmental, human resources, banking and media.
About the author
Benjamin Miller
Customer Facing Data Scientist at DataRobot
Ben Miller is a Customer Facing Data Scientist at DataRobot with a strong background in data science, advanced technology, and engineering. Ben is a machine learning professional with demonstrable skills in the area of multivariable regression, classification, clustering, predictive analytics, active learning, natural language processing, and algorithm R&D. He has scientific training and application in disparate industries including; biotechnology, life sciences, pharmaceutical, environmental, human resources, banking, and media.










