こんにちは、DataRobotのデータサイエンティスト伊地知晋平です。
今回、2018年7月に開催しましたワークショップ「機械学習を使った要因分析」でご紹介させていただいた内容を元に、山本祐也さんと分担して3本のブログを書きました。3週に渡って、「理論編 Part 1 (8/13公開)」「理論編 Part 2 (本ブログ)」「実践編 (8/27公開)」をアップしてまいりますのでお楽しみいただければ幸いです。
上記リンク先には、ワークショップで使用したプレゼン資料やハンズアウトで使ったサンプルデータがアップされています。DataRobotユーザーの方はぜひご活用ください。
※理論はあと回しでいいからまずはDataRobotで要因分析をどうやるのか知りたい、という方は、山本さんのブログ「機械学習を用いた要因分析 – 実践編」(8/27公開)をご参照ください!
因果解析:観察データから因果に迫る!
理論編 Part 1 において、
- 機械学習による予測モデルは、因果関係を表現しているわけではない
- しかし、機械学習モデルからは因果仮説を具体的に検討するために有用な情報を得られる
- したがって、ドメイン知識の助けがあれば、結果に影響を与える本当の要因を推定できる場合がある(というか結構多いよ)
と書きました。しかし、もしどうしても正しく因果関係をモデル化したい、というモチベーションがあれば(そしてそのための投資が正当化できるのであれば)、下図のように、実験を行うのが本当の因果関係を明らかにするのに最も確かな方法です。(実験のやり方を工夫すると、最小の試行回数で最大の情報量を獲得して正確なモデルを作ることができますが、そのための手法と理論の体系は実験計画法と呼ばれており、工業分野でよく利用されています)

しかし、1回の実験にかかるコストが大きい、あるいは倫理的に許されない、等の理由で、現実世界で実験を行うのが困難な場合も多いでしょう。(例えば、同程度に重篤な病気の人のうち半分だけに手術をする、というような研究はできない)
そこで、すでに取られたデータの観察研究により因果関係の推論を試みるのが、これからご説明する因果推論のアプローチになります。ところで上図をよく見ると、「交絡因子」という言葉が何度も出現していますね。実は因果解析のキープレイヤーは交絡因子なのです。
以下は「販促キャンペーンを打つ/打たない」の2値をとる要因Xと「店舗売り上げ」なる結果変数Y、XとYの両方に影響を与える要因と考えられる交絡因子Zi (i=1,2,…,n)からなる因果ダイアグラムです。因果解析の観点からは、「店舗で販促キャンペーンを打つ、という介入には本当に店舗売り上げを増加させる因果効果があるのかどうか」を検証することになります。
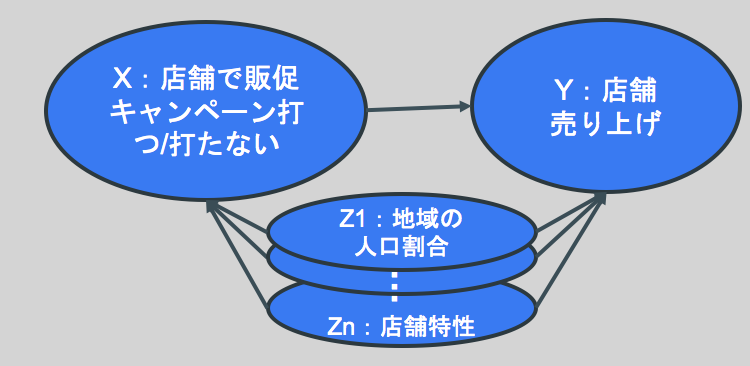
この時、Xだけを取り上げて、「販促キャンペーンを打った店舗の売り上げ平均値」と「販促キャンペーンを打たなかった店舗の売り上げ平均値」を単純に比較した時に差があったとしても、それが「キャンペーンを打ったことによる因果効果だ!」とは言い切れません。なぜなら、もし下図右側のように、Zの値(例えば地域の高齢者人口割合)に応じてキャンペーンを打つ/打たないが決まっていたのであれば、売り上げの増加という効果が要因Xによるものなのか交絡因子Zによるものかの区別がつかないからです。
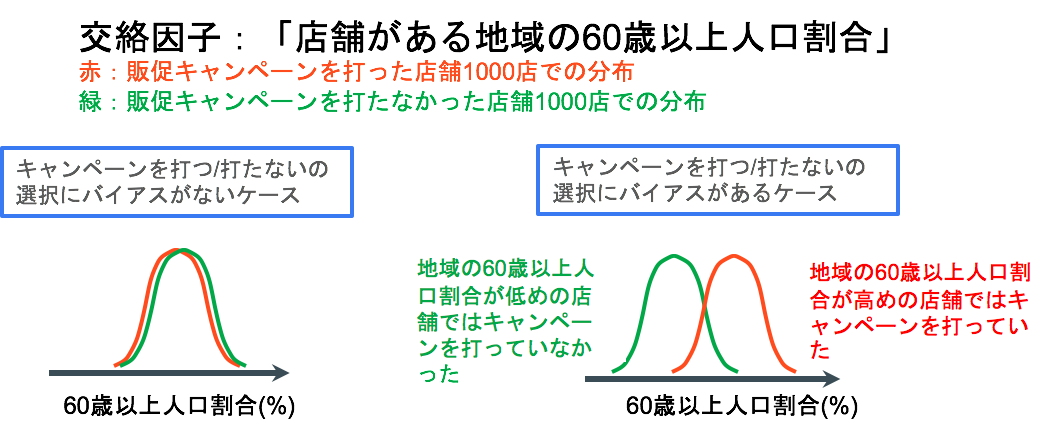
このように交絡因子の影響で要因Xの値が決まっている状態を選択バイアスと呼ぶのですが、要因Xから結果Yへの因果効果をフェアに推定するためには、交絡因子による選択バイアスが生じていない状態で比較を行わなければなりません。
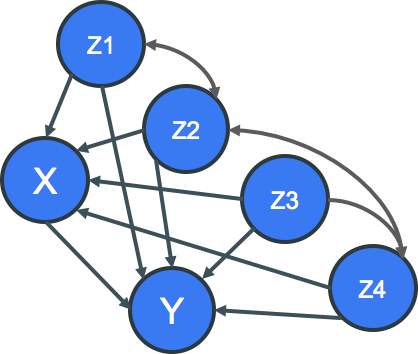
一つの交絡因子による選択バイアスを考えても上記のように複雑なのに、現実世界では下図のように複雑な絡み合いが交絡因子と要因Xや結果Yとの間で、あるいは交絡因子同士で起こっていると考えるのが自然です。この複雑な世界で、ある要因Xが結果Yに及ぼす本当の因果効果をいったいどのように推定すれば良いでしょうか。交絡因子を1個1個取り上げて考えるのはとても難しそうだなというのが率直な感想です。
傾向スコアを使った因果効果の推定
そこで、「傾向スコア」(Rosenbaum & Rubin, 1983)の概念を導入し、複数の交絡因子による選択バイアスを一つの変数に縮約させて、この課題を解決しましょう。
傾向スコアとは、「0, 1」の2値をとる要因Xの、1(正例)の発生しやすさを表す確率変数です。実務において細かい理論を理解する必要はありませんが、傾向スコアを算出する時には、注目している要因Xをターゲット、交絡因子Zi(i = 1,2,…,p)を特徴量(説明変数)とする予測モデルを利用するとだけ覚えておいてください。2値変数をターゲットとする予測モデルとなると、ロジスティック回帰から一般化加法モデル、サポートベクターマシン、勾配ブースティグ、さらにはニューラルネットワークまで、DataRobotを使えば様々なモデルの中で与えられたデータから最も精度の良いモデルを作ることが可能です。具体的なやり方は山本さんのブログ(8/27公開)で丁寧に解説されています。
傾向スコアをDataRobotで計算したら、次に「傾向スコアマッチング」を行います。これは1次元に縮約された傾向スコアの分布を見て、その選択バイアスを解消するようにうまくデータサンプリングを行う作業です。こちらも様々な手法が提案されていますが、目指していることは下図のようなイメージです。右側のヒストグラムでは要因Xが0群ヒストグラムと1群ヒストグラムを比較して選択バイアスが無くなっているとわかります。(傾向スコアマッチングはDataRobotの外で行っていただく作業ですが、山本さんが作成されたPythonスクリプトを使えば簡単に実行できますのでぜひご利用ください)
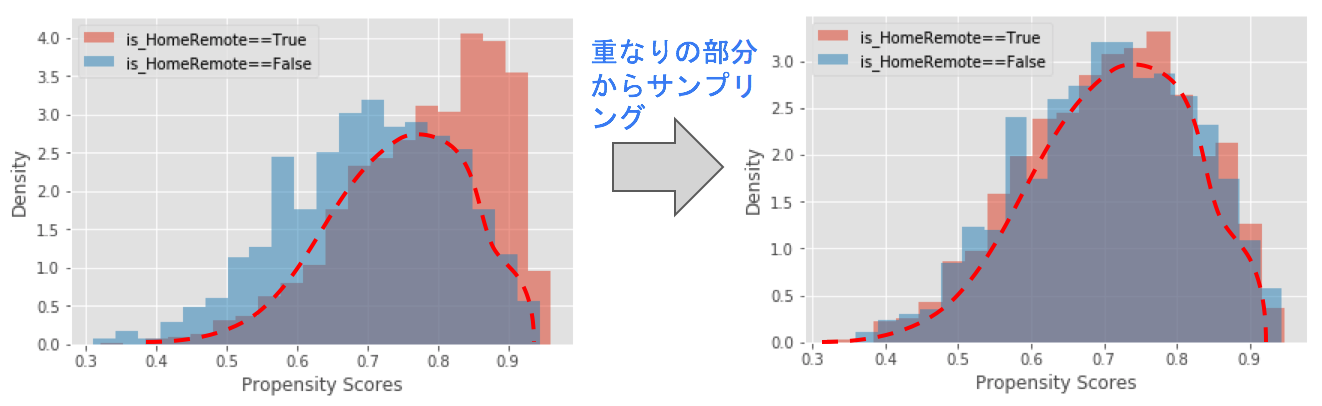
さて、傾向スコアマッチングを行ってダウンサンプリングしたデータに対して、要因Xと結果Y、さらに複数の交絡因子を一つにまとめた傾向スコア”PS”により、下図のようなシンプルな因果ダイアグラムを考えられます。(傾向スコアマッチングにより選択バイアスが小さくなっているので、PSからXへの因果効果はかなり0に近い値になっていることが期待されます)
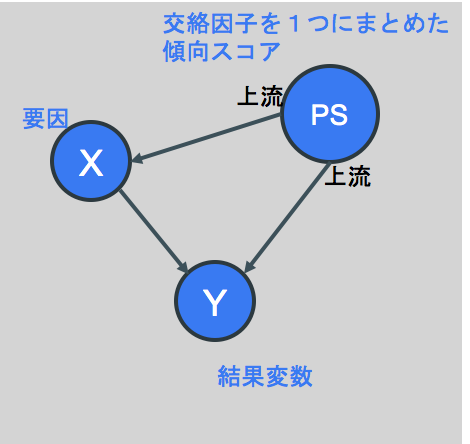
この時、Yをターゲット、XとPSの2変数を特徴量とする予測モデルを生成すると、そのモデルにおけるXとYとの相関の強さは、XによるYへの因果効果と判断できます。(理論背景についてご興味あれば参考書籍2「岩波データサイエンス Vol.3」を参照ください)
傾向スコア計算に使用する交絡因子の選び方
さて、本ブログの最後に、傾向スコアを計算する際に解析に用いる交絡因子をどのように選択するかの基本方針をご紹介します。近年、傾向スコアは医学/計量経済学などの分野での学術研究でも因果解析のスタンダードアプローチとして使われるようになっていますが、弱点を一つ挙げるとすれば、「傾向スコア計算時に取り上げなかった交絡因子の影響を考慮できない」です。
(なお、アドバンストな話になりますが、実験計画法やランダム化比較試験(RCT)は、「実験時に取り上げなかった交絡因子の影響」も含めて比較する形で因果効果の本当の大きさを推定できるため、観察研究による因果推論よりも、さらに厳密に因果効果を推定できる方法です)
そのため、実は交絡因子の適切な選択にこそ、要因分析・因果解析から意味のある知見を得られるかどうかがかかっていると申し上げても過言ではありません。以下のガイドラインを元に、観察研究の前にドメインエキスパートと交絡因子について十分検討されることを強くお勧めします。
- 何でもかんでも選んではいけない:要因Xと結果変数Y両方に影響を与える(時間的・物理的に上流)と考えられる因子のみ
- 要因Xに対する選択バイアスがあると考えられる因子のみ
- 交絡因子同士の多重共線性(マルチコ)は気にしなくても良い(傾向スコアを算出する際にはモデルの予測精度のみに主眼が置かれるので、交絡因子同士の多重共線性は考慮しなくても大丈夫)
結言
以上、「機械学習による要因分析-理論編 Part2」をお読みいただきありがとうございました。ぜひ山本さんのブログ「機械学習を用いた要因分析 – 実践編」(8/27公開)もご覧いただき、DataRobotで簡単に要因候補の絞り込みや傾向スコアの計算ができることをご実感下さい!
2018年7月のセミナーでご紹介しました結言を以下に示して、山本さんに繋ぎたいと思います。

参考書籍
本ブログ作成にあたっては、下記書籍を参考にしました。要因分析/因果解析についてもっと勉強したいと思っている方に、2018年8月時点で最も推薦できる良書です。
1.データ分析の力 因果関係に迫る思考法 (光文社新書), 伊藤 公一朗 (著)

2.岩波データサイエンス Vol.3, 岩波データサイエンス刊行委員会 (編集)

オンデマンドビデオ
AI Experience Virtual Conference 2021
「DataRobot AI Cloud」に関する基調講演や、業界をリードするDX推進企業の取り組み、AIサクセスを実現するビジネスリーダーによるパネルセッションをオンデマンドビデオで確認
オンデマンドで見る















