機械学習モデルがどの特徴量から学習したか
DataRobotのデータサイエンティスト、緒方良輔です。
この記事では、機械学習のモデルが投入されたどの特徴量を重視して学習を行なったかを評価する方法についてお話ししたいと思います。
ビジネスやR&Dの現場で機械学習を利用する際には、投入したどの特徴量がターゲットを予測する為に重要かを、学習したモデルを観察して理解しようとするシーンは多く見られます。後の例でも用いますが、金融機関での与信リスクの計量分析を行うことを考えてみます。過去のデータから貸し倒れ率を予測する様なモデルを作成し、与信を実施する際の判断に使うという内容です。
おそらく出来上がったモデルは、与信対象のクレジットヒストリや年収などの特徴量を重視して学習している事が想像できます。同時に、住所などの情報が貸し倒れ率の予測に大きく貢献している、といった、直感的でない情報が出来上がったモデルから発見されることもあるかもしれません。その場合は与信の際、関連する情報をより詳しく取得するなどといった工夫で、さらに精緻な予測ができるようになるかもしれません。
前者の確認にも、後者の発見にも、モデルがどのような特徴量を重要視しているか、という指標が必要です。では、どの様にモデルにとっての特徴量の重要度を評価すればよいでしょうか。
モデルに投入した特徴量が有効だったかを評価する際、例えばランダムフォレストの様な木系のアルゴリズムを用いたモデルであれば、Gini不純度を用いて重要度を測るかもしれません。しかし、回帰系のアルゴリズムにはその様な指標はありません。かわりに特徴量ごとの係数やその有意性が計算でき、ある特徴量がモデルにとって重要かどうかの判断材料にはなるものの、その特徴量を投入したことによってどれだけ予測が助けられているか、という順序づけには向きません。
本記事ではまず、アルゴリズムに依存した形での特徴量の評価手法はどのようなものがあるかについておさらいをした後、アルゴリズムに依存せずに特徴量の重要度を統一的に評価できる方法としてPermutation Importanceをご紹介します。他の方法に比した優位性や計算方法、Pythonパッケージの使い方、DataRobotにおける位置付けなどについても触れたいと思います。
特徴量の重要度を評価する様々な手法
単に機械学習とは言っても、木系のもの、回帰系のもの、ニューラルネットワークのような階層的なものなど、今日ではたくさんのアルゴリズムが存在します。そして、ある特徴量がどれだけモデルの学習に際して重要視されたかという指標は、多くの場合アルゴリズムに依存した形で計算されます。
木系の代表的なアルゴリズムであるランダムフォレスト(もしくは、こちら)では、訓練データから重複ありでの抽出を繰り返すブートストラップ法によりデータを複数個に複製し、それを用いて多数の決定木を作成します。この操作はデータから重複ありでランダム抽出を行うという特性から、平均3割程度のデータがOOB(out-of-bag)という形で学習に利用されません。ランダムフォレストではこういったデータをモデルの精度の評価に用いたりもしますが、ある特徴量をランダマイズしたとするとこの精度がどれだけ押し下げられるか、という方法でMean Decrease in Accuracyと呼ばれる特徴量の重要性を表す指標を計算することもできます。また、同じ木系のアルゴリズムに適用できる、視点の異なった評価としてMean Decrease in Giniという指標もあります。決定木やランダムフォレストの様に決定木を弱学習機として用いる他のアルゴリズムでは、木のノードに使う特徴量を決める際Gini不純度(もしくはエントロピー)を用います。このGini不純度は各ノードが受け取ったデータ内でどれだけターゲットが分類されず混ざっているのかを表しており、データがノードを通過した際にそれがどれだけ改善したかという視点でモデルに対する特徴量の重要性を評価するのがMean Decrease in Giniです。
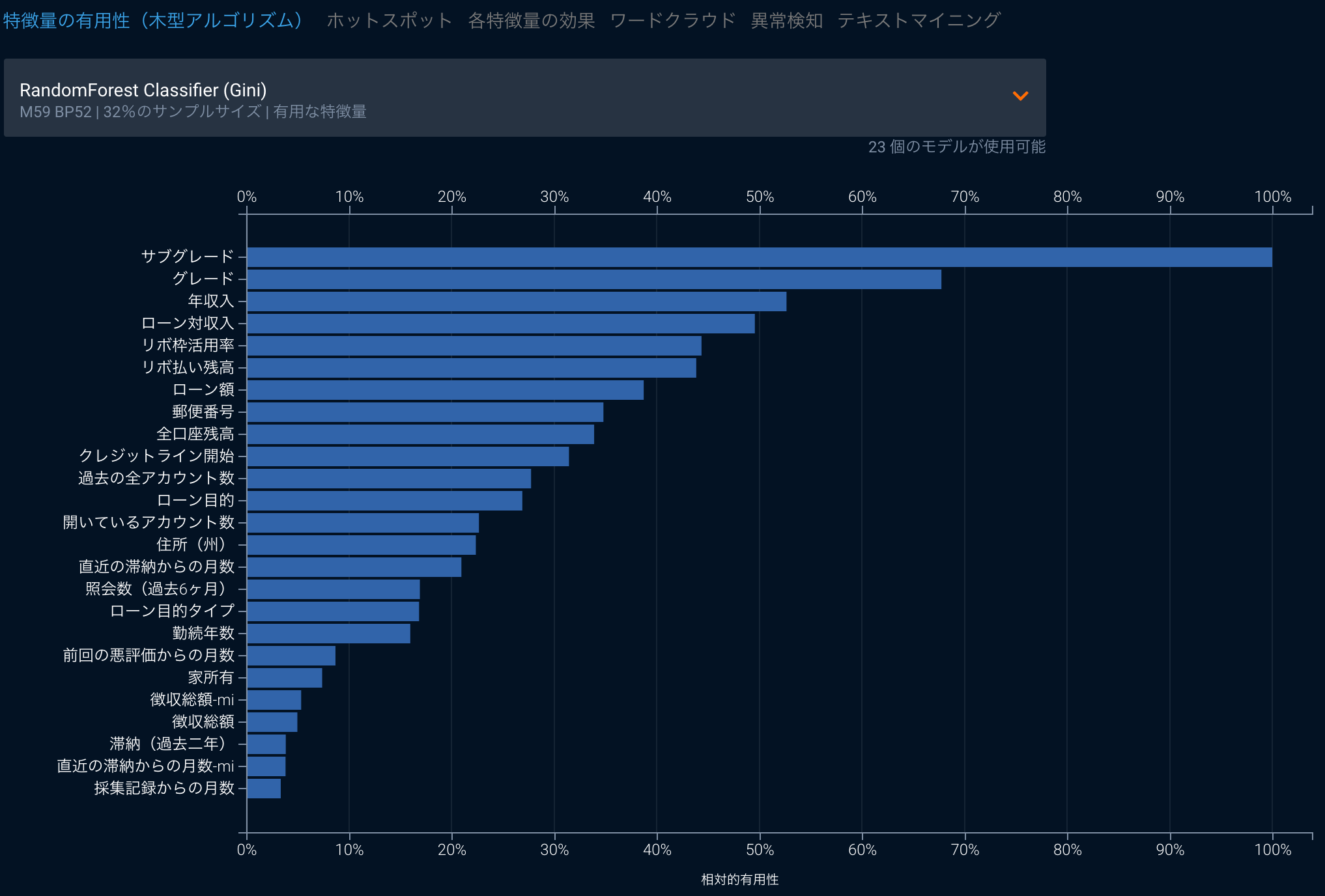
他には回帰系のもっともシンプルなアルゴリズムである回帰分析では、特徴量ごとに回帰係数と、その有意性を計算することができます。これらの指標は直接的にモデルがその特徴量を重視して学習したかどうかに答えているわけではありませんが、少なくとも回帰係数が有意であれば、その回帰係数に対応する特徴量の変動が被説明変数と共変していることがわかります。
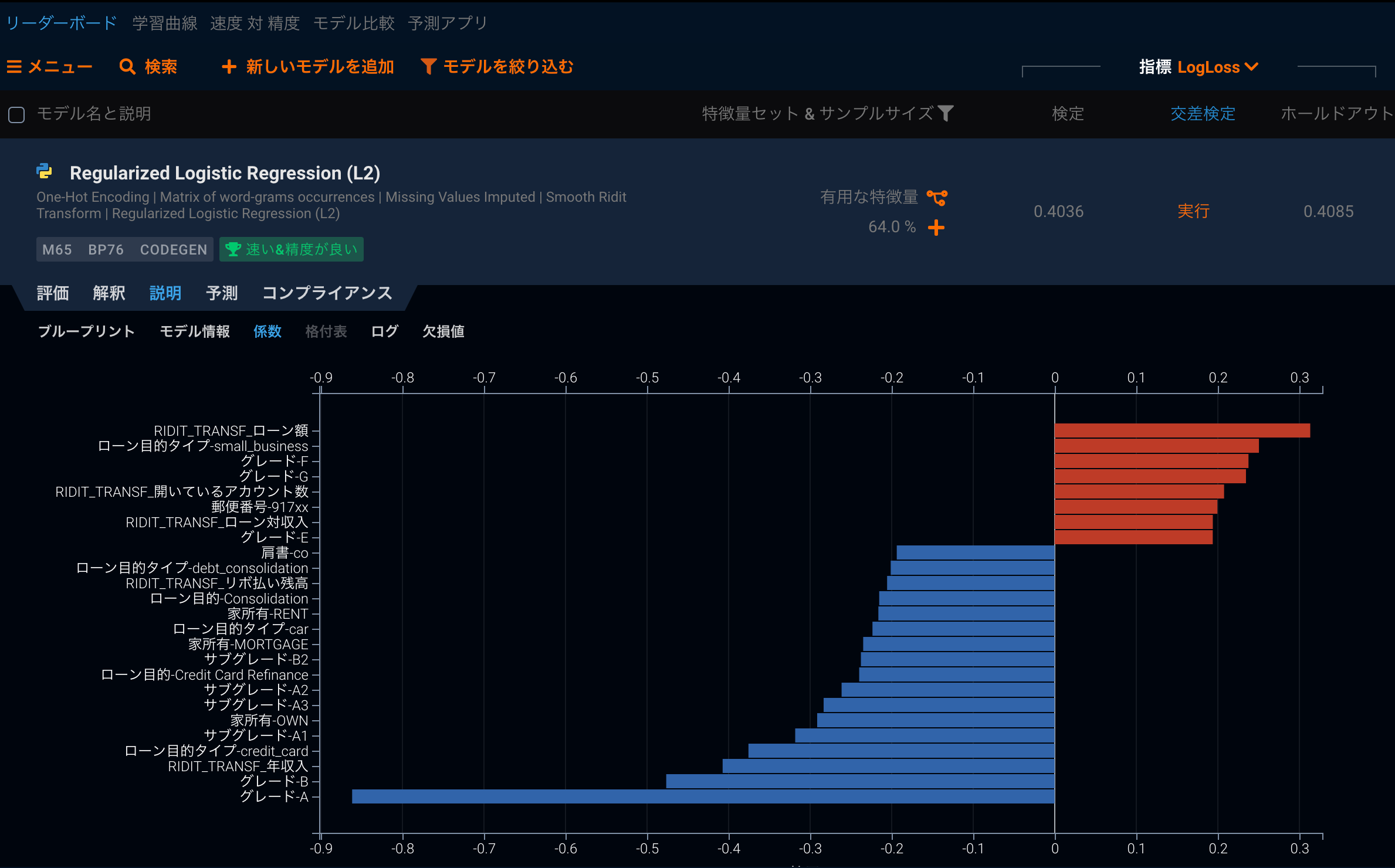
なお、ニューラルネットワークの様な階層的なアルゴリズムでは、この様なモデルにとっての特徴量の重要性を計算することが一般的には困難であることが知られており、今日でも強い興味を集めている重要な研究テーマとされています。最新の研究はこちらの論文などによくまとまっているので、気になる方はぜひ目を通してみてください。
Permutation Importanceの導入
さて、本題であるPermutation Importanceについて説明しましょう。今回のメイントピックであるPermutation Importance(参考:Fisher, Rudin, and Dominici(2018))は、モデルにとってのある特徴量の重要度を、「ある特徴量がどれだけモデルの予測精度向上に寄与しているのか」と解釈して計算されます。
この重要度を測るために、Permutationと呼ばれる手法を用います。非常に単純な手法で、ある特徴量をランダムに並べ替えてしまうだけです。ある特徴量を完全にランダムに並び替えたとすると、その特徴量はどんなものでももはやターゲットを説明する能力はありません。例えば与信の貸し倒れ確率をターゲットとして予測する場合を考えると、与信対象の信用グレードや給与などと言った非常に関連が強く説明力が高そうな特徴量でも、Yさんの信用グレードを参考にして全く無関係のXさんの貸し倒れ率を予測できないことは明白です。
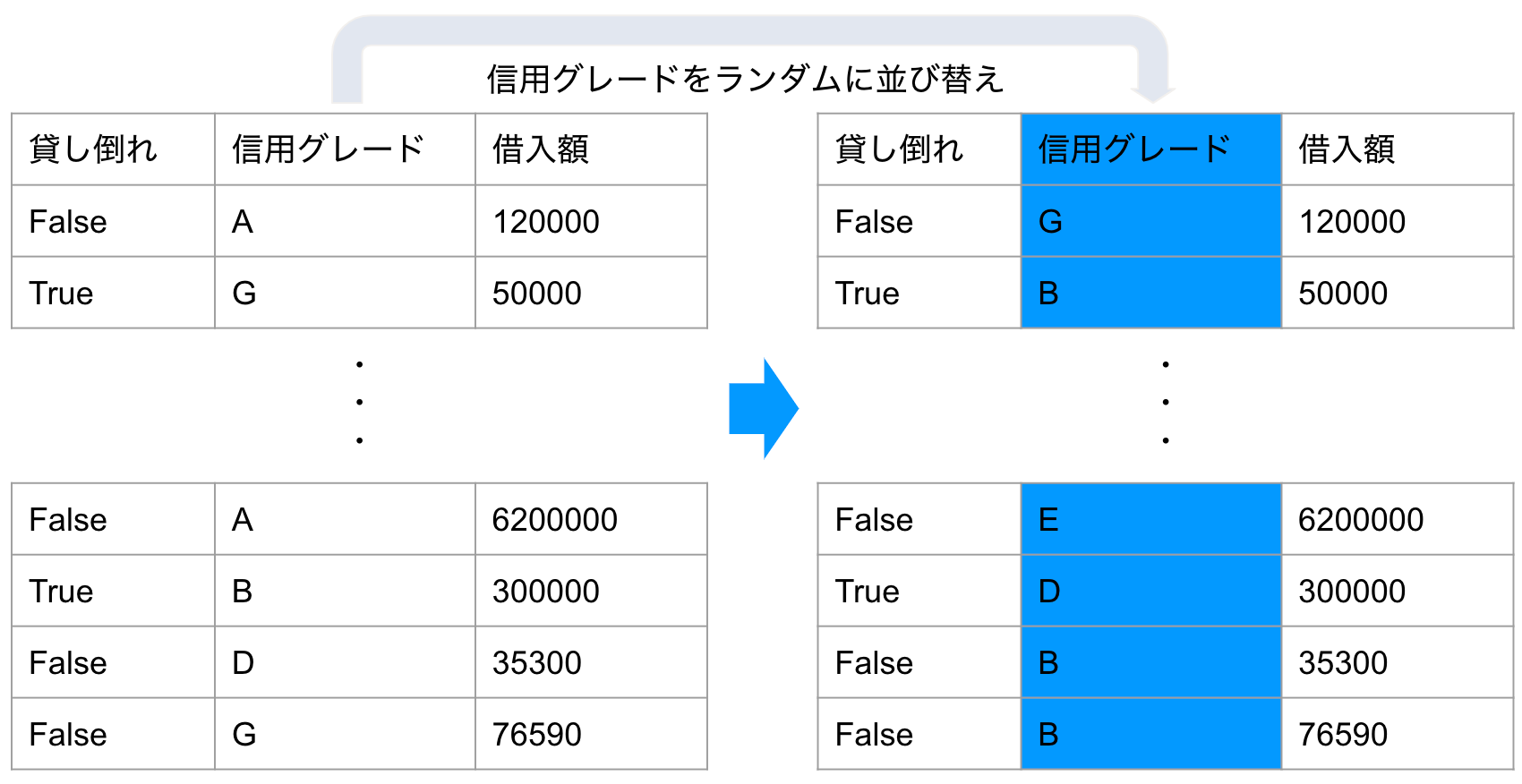
Permutationの日本語訳を辞書で引くと「順列」や「並べ換え」とでますが、まさに並び替えて順列をばらばらにする、という操作を行っています。仮にモデルの中のある特徴量をランダムに並び替えて予測を行なった際の誤差が、もともとのモデルよりも誤差が大きかったとしましょう。その際には、大きくなってしまった誤差ぶんだけ、ランダム化された特徴量がもともとのモデルの精度に寄与していたと考えることができます。
そしてランダム化された特徴量で作ったモデルの誤差をもともとのモデルの誤差で割ったものがPermutation Importanceです。同じ手順をモデルの中の全ての特徴量に対して行えば、どの特徴量がもっともモデルの精度に寄与しているか、もしくは精度に寄与していないのかを理解することが可能です。
勘の良い方はすでにお気づきと思いますが、先ほど触れたMean Decrease in Accuracyもこの方法を用いて、OOBのデータに対する予測力の低下量を測ることで計算されています。Permutation Importanceの優位性は、精度の低下度合いの検証をテストデータを用いて行うことで、テストデータを確保してモデリングをしていればどのような形のアルゴリズムを用いたモデルに対しても計算することが可能な点です。
実は、この優位性は実際のビジネスで機械学習を適用する上で非常に重要です。なぜならば、特徴量の重要度に限らず、モデルの解釈に必要な操作がアルゴリズムの形に依存しないということは、アルゴリズムの選択をデータの質や量、状況に応じて選択できるようになるということだからです。すでに申し上げた様に、今日にはたくさんのアルゴリズムがありますが、全てのアルゴリズムは決して汎用ではなく、得意な状況や苦手な状況があります。その為、アルゴリズムの選択は状況に応じて適切に行うことが重要です。その際に、統一的なアウトプットでモデルの解釈やレポーティングを行えるPermutation Importanceを利用することで、アルゴリズムごとの差異がその利用の障壁にならないような工夫をすることができます。
Permutation Importanceの使い方
具体的なPermutation Importanceの計算は以下の手順で行われます。
学習済みモデルをf, 特徴量行列をX, ターゲットベクトルをy, 損失関数(例えばMSE)をL(y,f)としたとき
- 本体のモデルを用いて、誤差eo = L(y, f(X))を計算する
- 全ての特徴量j = 1,…,Jに対して、
- jをpermutationすることで特徴量行列Xpjを計算する
- 上記を用いて、permutation後の誤差ep = L(y,f(Xpj))を計算する
- Permutation Importance PIj = ep/eoを計算する
上記の手順で計算したPermutation Importanceが大きければ大きいほど、特徴量jがモデルにとって重要であることがわかります。
先ほど、着目する特徴量をばらばらに並び替えることで、その特徴量のターゲットへの説明力を無くしていると説明しましたが、これは特徴量を落とすことと予測精度への影響という意味で等価です。その上で、実際に特徴量を落として都度モデルを作り変える場合に発生する、必要な計算量が膨大になり現実的な利用が難しいという問題を、Permutationという方法を採用することで解決しています。
いくつか利用上の注意も述べておきたいと思います。
代表的なものとして、相関の高い特徴量を同時にモデルに投入している際にはどちらかの特徴量があまり評価されないという問題が起こります。これは特徴量の重要度をモデルへの精度向上にどれだけ寄与しているかで測っている為です。例えば非常に似た様な振る舞いをする郵便番号と住所という特徴量を同時にモデルに投入した場合を考えると、前者をランダム化したとしても後者の特徴量によって前者から学習すべき内容がほとんど学習できてしまう為、精度があまり下がりません。精度が下がらないので、その特徴量がターゲットに対して高い説明力を持っていたとしても重要度が低いと計算されてしまいます。
重要度を用いて特徴量選択を行う際、他の指標と比べて重要度の定義がどの様に違うかにも注意が必要です。
- 具体的にはGini不純度を用いた指標に比べると、Permutation Importanceはおおむね全体への影響は小さいものの局所的な影響が強い特徴量への感度が低い
- 例えば売上高の予測に対するクリスマスセールフラグは、セール期間がそもそも限定的なため精度に対する影響を見るPermutation Importanceでは影響が小さいが、局所的にはデータの分類に影響するためGini不純度を用いると比較的大きく算出されます
- 数値特徴量の重要度が他方より高く算出される傾向にある
- Gini不純度で計算をすると数値特徴量は境界の付近では不純なデータがより残る傾向があるので、数値特徴量への重要度はカテゴリカルな特徴量よりも比較的低く算出される傾向にあります
またPermutation Importanceからさらにインサイトを引き出すには、投入する特徴量のデザインについても気を配っておくと良いでしょう。例えば先ほどの貸し倒れ予測の例で、ある人の年収と在職期間が予測に有用な特徴量であるとします。その際、2つのかけ算で累積年収という特徴量にして評価してみることで、特徴量とターゲット間の関係がよりよくわかるかもしれません。他にも、特徴量には必ず一目でどんなものかわかりやすい名前をつけておく(決済手法_a残高、ではなくリボ払い残高と変換する)ことなども重要なポイントです。
実際に利用する際には、pythonユーザーであればeli5というパッケージをお勧めします。pythonでの機械学習モデリングに非常によく利用されるscikit-learn(sklearn)のモデリングプロセスにシームレスに繋がる様に設計されており、リンク先にもある様に下記の様なコードで非常に簡単に利用できます。
import eli5
from eli5.sklearn import PermutationImportance
from sklearn.svm import SVC
# … load data
svc = SVC().fit(X_train, y_train)
perm = PermutationImportance(svc).fit(X_test, y_test)
eli5.show_weights(perm)
また計算したpermutation importanceを表示させるだけでなく、sklearnに返すことで特徴量選択に使うことも可能です。もちろん、sklearn以外にも利用可能です。
なお完全な余談ですが、eli5(Explain me like I’m 5)というのはスラングで、5歳児にもわかるように説明してくれ、という意味です。
DataRobotにおけるPermutation Importance
もちろんDataRobotにおいてもPermutation Importanceは簡単に利用でき、より便利に利用する為に様々な工夫が凝らされています。
例えば、先に説明した振る舞いが似通った特徴量が投入されている場合、DataRobotではある特徴量が他の特徴量の存在により重要度が低く算出されている可能性があるという警告を行なってくれます。下記の例の場合は「採取記録からの月数」というデータが他のデータの振る舞いと非常に似通っていることを警告しています。この場合、警告が表示されている特徴量を削除することで、他の特徴量の重要度を正当に評価することが可能です。
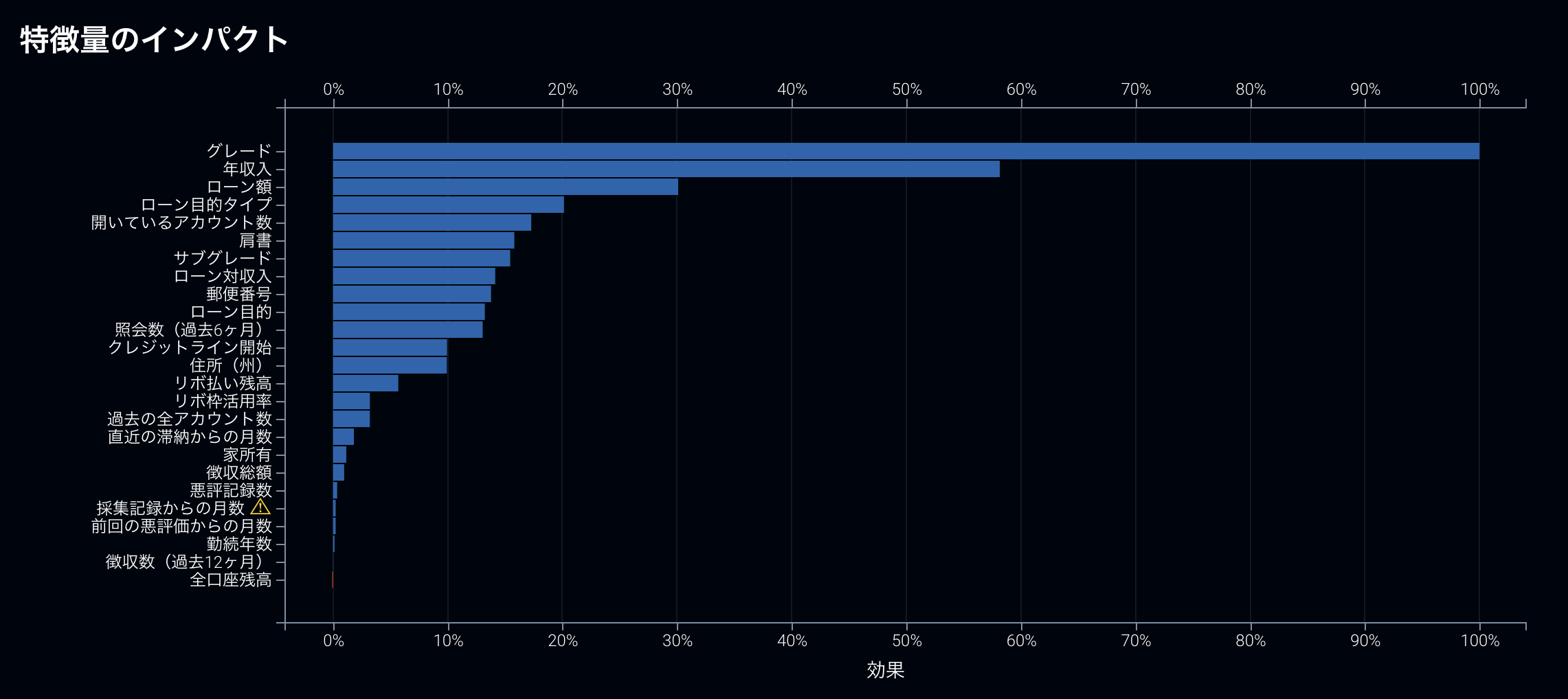
他にも、時系列モデリングを行なった際にはラグ変数を大量に生成する為に投入された形での特徴量(入力特徴量)単位での重要度を理解しにくいという問題がありましたが、モデリングに使う形での特徴量から、入力特徴量単位に変換してくれる機能なども実装されました。
モデリングに使われた、ラグ変数などを含む特徴量単位での表示
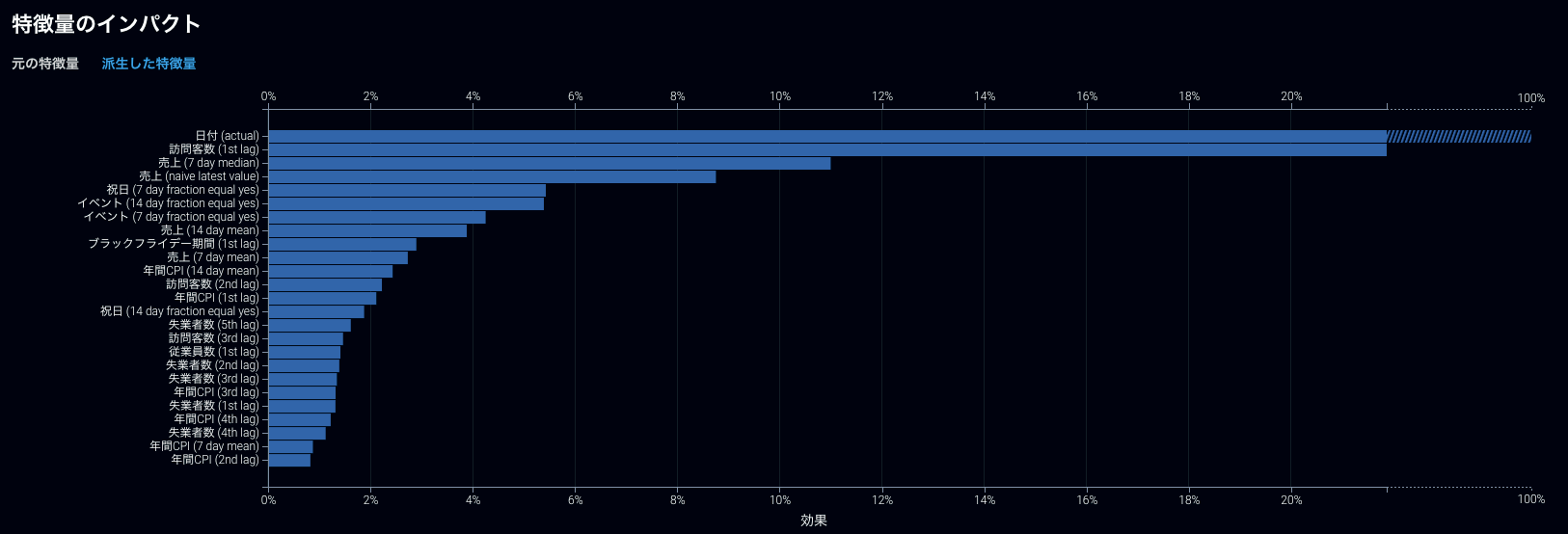
ラグ変数などを入力特徴量単位でまとめた表示
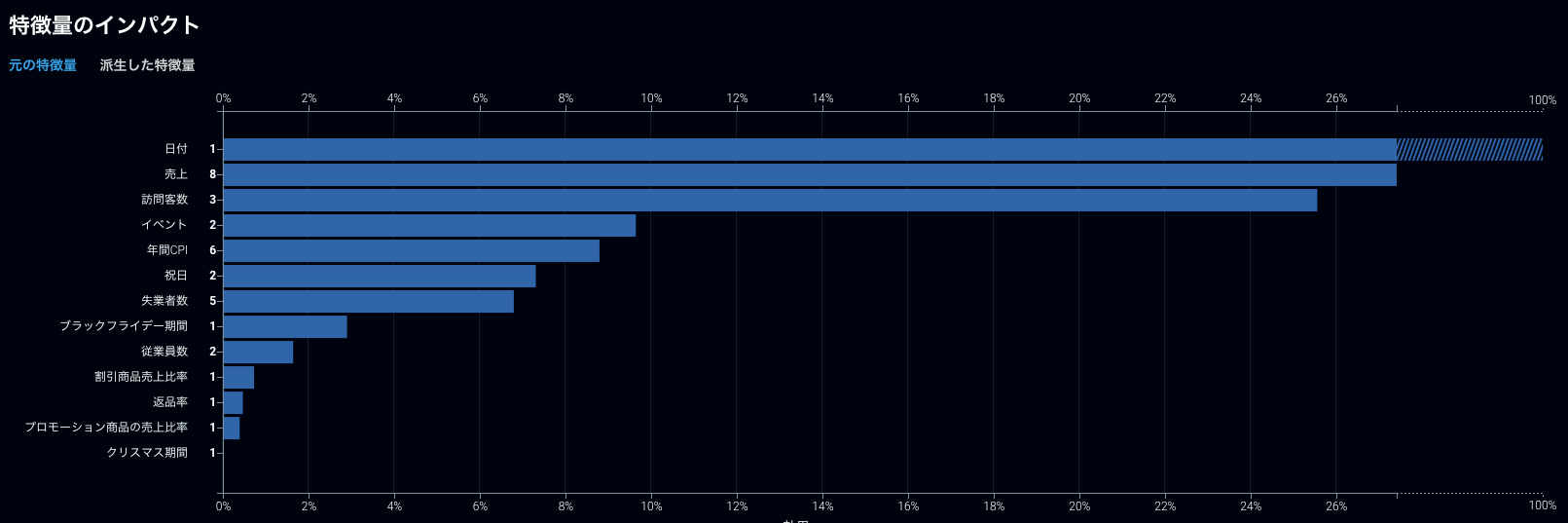
また、これまで説明してきたPermutation Importanceだけでなく、アルゴリズムに依存しない形でモデルの解釈を行う他の機能も多く揃っており、特徴量がどのように予測結果に影響を及ぼしているのかを測る部分依存と呼ばれる機能がその代表です。
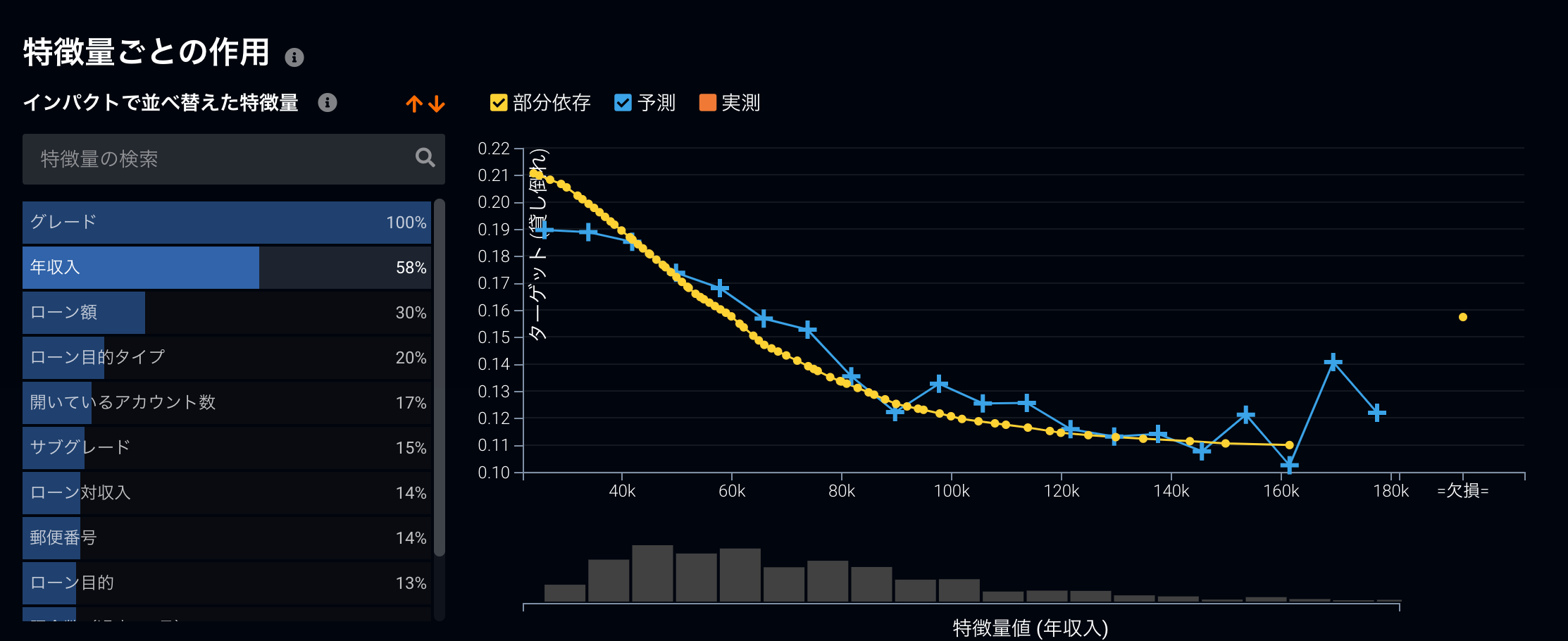
こちらも非常によいモデルの解釈ツールなので、リンク先のブログ記事もご覧いただけると参考になるかと思います。
モデルの解釈とアルゴリズム
ここまでPermutation Importanceという特徴量の重要性を測る尺度について説明をしてきました。結びとして改めて述べておきたいのは、ビジネス上での機械学習モデルの運用に当たって必須になるモデルの解釈は、アルゴリズムに依存しない汎用的な形で行うことができる方法がきちんと発展してきているということです。その様な手法を積極的に活用していくことで、「得意だから」であったり、「この方法でレポートをしてきたから」という様なビジネスにおけるデータサイエンスの活用に本質的に関係のない方法でアルゴリズムの選択を行なってしまう自体を避けることができます。様々な状況に対応できる、汎用性の高い道具立の一つとして、ぜひこのPermutation Importanceもご活用いただけると嬉しいです。
オンデマンドビデオ
AI Experience Virtual Conference 2021
「DataRobot AI Cloud」に関する基調講演や、業界をリードするDX推進企業の取り組み、AIサクセスを実現するビジネスリーダーによるパネルセッションをオンデマンドビデオで確認
オンデマンドで見る












