Colin Priest is a Fellow of the Institute of Actuaries of Australia and has worked in a wide range of actuarial and insurance roles, including Appointed Actuary, pricing, reserving, risk management, product design, underwriting, reinsurance, relationship management, and marketing. Over his career, Colin has held a number of CEO and general management roles, where he has championed data science initiatives in financial services, healthcare, security, oil and gas, government and marketing. He frequently speaks at various global actuarial conferences.
Colin is a firm believer in data-based decision making and applying machine learning to the insurance industry. He is passionate about the science of healthcare and does pro-bono work to support cancer research.
One of the questions actuaries often ask me is “How does machine learning identify outliers in data?” or “What does machine learning do with outliers?”
The traditional statistical models that actuaries typically use require a number of assumptions about how the data was created, the processes underlying that data, and the credibility of that data. Today I’m going to focus on credibility and outliers.
In statistics, an outlier is a value that is extreme and doesn’t fit the general pattern. Outliers may indicate problems in your data, and they may skew your models. But the definition of outliers suffers from being subjective. For example, I have some auto/motor insurance data, and I have plotted sum insured versus claim severity. Is the highest sum insured, marked in red, an outlier? One could argue either yes or no to this question.
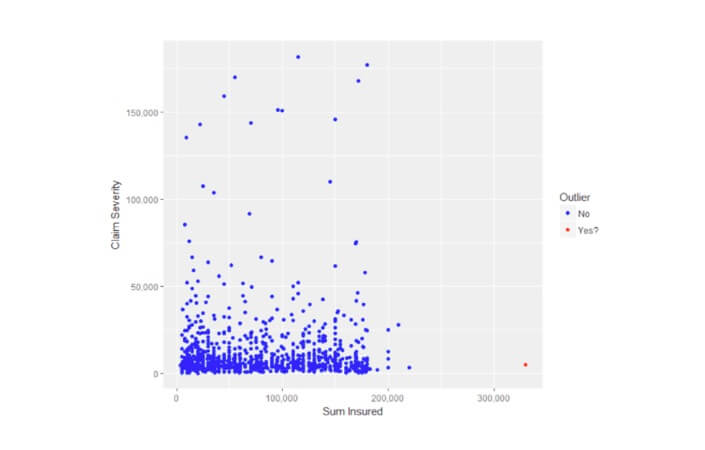
Even if a data point is an outlier, it may not matter for the analysis. So in statistics they have developed the concept of “leverage.” Leverage is a measure of how far away the independent variable values of an observation are from those of the other observations. Statisticians can objectively measure leverage and its impact upon a linear model. If a single observation has too much leverage, then that single observation can change the model all by itself. That can be dangerous.
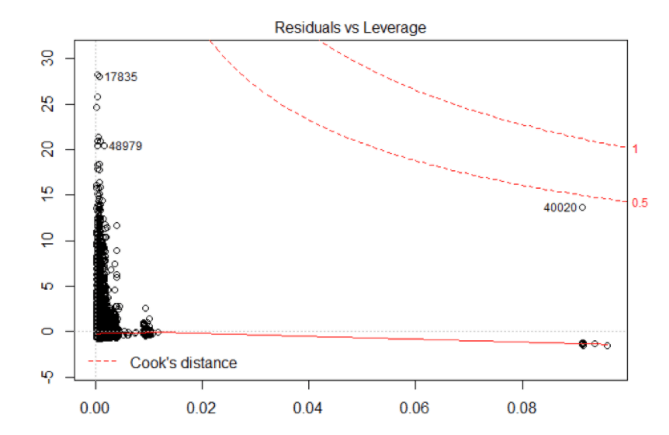
The plot above shows how R has used a statistical measure, called Cook’s distance, to flag observations in the data that have high leverage.
When I find data points with high leverage, I have three options:
- Remove the data point
- Give the data point less weight
- Leave the data point unchanged in the model
If I remove the data point, then I am removing data that may be important for future decisions. If I give the data point less weight, then I need to determine how much less weight to give it. There is no clear guidance on this. If I leave the data point unchanged, then I risk having a model that has been strongly skewed by luck.
As actuaries, we are taught about Buhlmann credibility, which says that smaller sets of data are less credible than larger sets of data. For example, if we toss a coin once and see heads, that doesn’t tell us much, but if we toss a coin 100 times and see 100 heads, then we have probably been using a two-headed coin! The reason that leverage causes problems is because the models that actuaries have been commonly using, generalized linear models (GLMs), are fitted using a technique called maximum likelihood, and this technique treats your data as 100% credible. Actuaries have started to notice this problem with GLMs, with the Casualty Actuarial Society publishing a paper entitled “Generalized Linear Mixed Models for Ratemaking: A Means of Introducing Credibility into a Generalized Linear Model Setting”.
Credibility weighting is particularly important when some of my model features are categorical. For example, in my sample auto/motor insurance data, there are only 12 Toyota MR2s, and one of them had a large claim. Just 12 records isn’t enough data to make a reliable estimate of the pricing relativity for MR2s. A GLM would incorrectly treat the actual results with full credibility and tell me that I need to price MR2s at tens of thousands of dollars per policy!
Machine learning approaches the problem of credibility and outliers in a different – and easier – way. In machine learning, we remove many of the restrictive assumptions that were required in traditional statistical models. Because machine learning fits very flexible algorithms, with high degrees of freedom, to historical data, they have to ensure that they don’t “overfit” the data, i.e., that they don’t give the data too much credibility. They have developed several techniques for doing this, including:
- Partionining the data and using out-of-sample data for testing models and tuning model hyperparameters
- Penalizing model coefficients, e.g. regularized generalized linear models
- Applying Buhlmann credibility to raw estimates for small categories within the data
These techniques result in models that are more predictive than GLMs and which automatically reduce credibility for outliers and small categories of data.
DataRobot’s automated machine learning platform makes this easy for me. Here’s what DataRobot does automatically for me:
- Partitions the data into train, validation and holdout buckets so that models are tested against different data to what they are trained on
- Optimizes the penalty for regularized generalized linear models
- Optimizes the model complexity for machine learning models so that they don’t over-train
- Finds the data pre-processing and machine learning algorithm that works best on new data
It’s easy, and I just let DataRobot do this mundane, time-consuming work for me. I trust DataRobot to figure out how much to trust my data.

About the author
Colin Priest
VP, AI Strategy, DataRobot
Colin Priest is the VP of AI Strategy for DataRobot, where he advises businesses on how to build business cases and successfully manage data science projects. Colin has held a number of CEO and general management roles, where he has championed data science initiatives in financial services, healthcare, security, oil and gas, government and marketing. Colin is a firm believer in data-based decision making and applying automation to improve customer experience. He is passionate about the science of healthcare and does pro-bono work to support cancer research.










